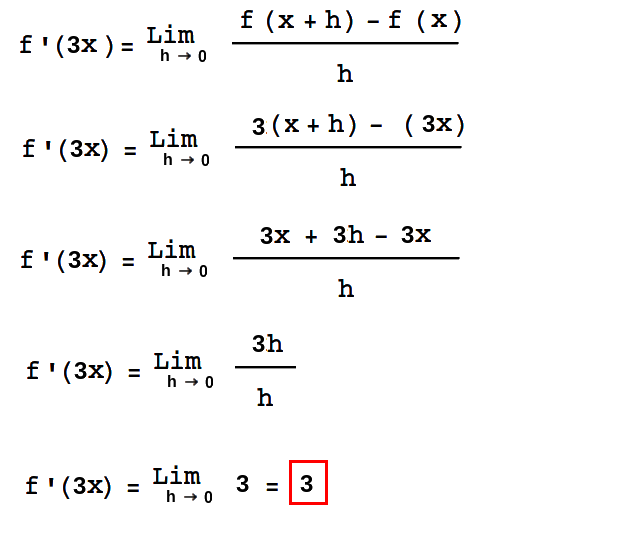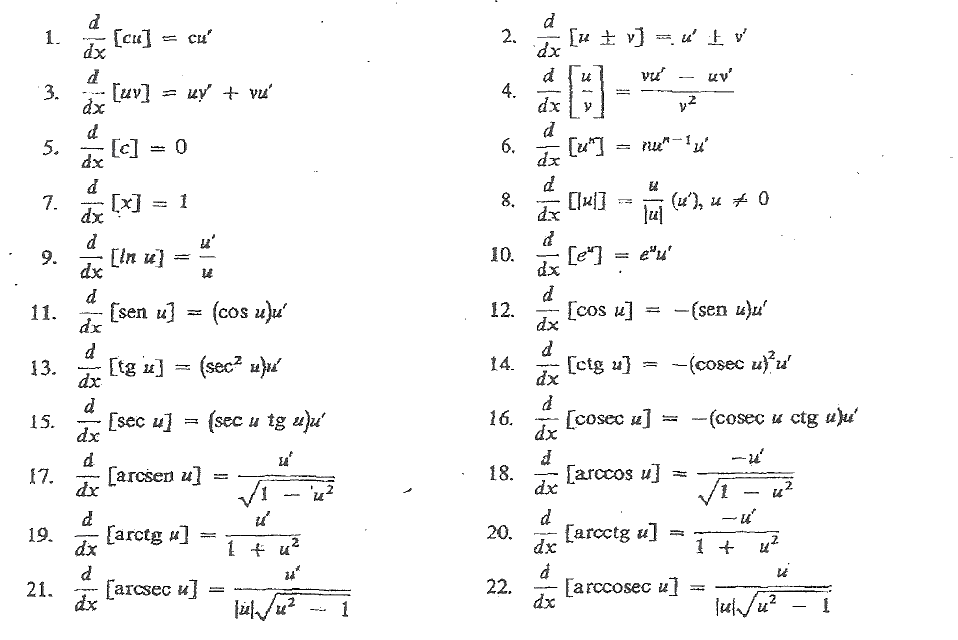Aprendamos
Derivadas
La derivada de una función es una forma de medir la rapidez con la que cambia el valor de dicha función matemática, según cambie el valor de su variable independiente. La derivada de una función se calcula como el límite de la rapidez del cambio de la media de la función en un cierto intervalo. El valor de la derivada de una función en un punto puede interpretarse geométricamente, debido a que se corresponde con la pendiente de la recta tangente a la gráfica de la función en un punto específico. La derivada de una función f en un punto x se denota como f´(x). La función cuyo valor en cada punto x es esta derivada es la llamada función derivada de f, denotada por f´. El proceso de encontrar la derivada de una función se denomina diferenciación, el área que trata con asuntos relacionados con las derivadas se llama cálculo diferencial.
La derivada es un concepto que tiene variadas aplicaciones. Se aplica en aquellos casos donde es necesario medir la rapidez con que se produce el cambio de una magnitud o situación. Algunas funciones no tienen derivada en todos o en alguno de sus puntos. Una función no tiene derivada en los puntos en que se tiene una tangente vertical, una discontinuidad o un punto anguloso.
Continuidad y diferenciabilidad
Una condición necesaria pero no suficiente para que una función sea derivable en un punto es que esta sea continua. Una función continua es aquella en la cual pequeños incrementos en los elementos del dominio de la variable dependiente produce pequeños incrementos en el valor de dicha función, de manera que cumpla:
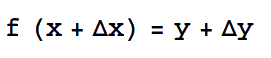
Haciendo estos incrementos cada vez más pequeños, las variaciones se hacen más pequeñas; cuando estos se aproximan a cero, en el límite,
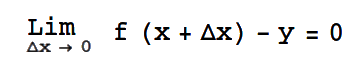
con lo que se obtiene, f(x)=y. Para un punto particular a, quiere decir que
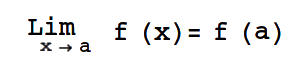
y si este último límite existe significa en consecuencia por un teorema de límites (un límite existe sí y sólo si los dos límites laterales existen y son iguales) que toda función f(x) que cumpla con
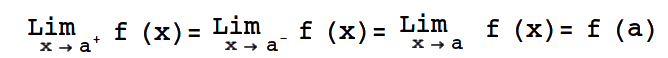
es continua en el punto a. Como consecuencia lógica, toda función derivable en el intervalo abierto I, es continua en I.
Derivada de una función
Considerando la función f definida en el intervalo abierto I y un punto a fijo en I, se tiene que la derivada de la función f en el punto a se define como:
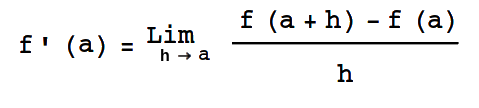
Ejemplo
Utilizando la función f(x)=3x definida para todo x perteneciente a los reales. Se va a calcular la derivada de esta fucnión.